4  Visualizações com plotnine

import pandas as pd
from plotnine import *

camaras = pd.read_csv('https://github.com/jtrecenti/main-cdad2/releases/download/data/camaras.csv')

4.1 Introdução

Nessa parte, nosso interesse é trabalhar na escolha das melhores visualizações para nossos dados, e como implementar isso usando a biblioteca plotnine.

Por que isso é importante? Além de realizar análises de dados, precisamos nos preparar para comunicar resultados. Boas visualizações são essenciais para isso. A necessidade de comunicar dados pode acontecer dentro do dos seus estudos de direito, mas também em situações de negócios, como apresentações para clientes e visual law.

4.1.1 O que é?

Visualização de dados é a representação de dados em gráficos, tabelas e diagramas que podem ser interpretados por pessoas. Trata-se de uma área interdisciplinar, misturando estatística, arte e comunicação. É uma parte da área de data storytelling, que envolve organizar todos os resultados de uma análise de dados em uma ordem lógica para comunicar de forma efetiva com a audiência.

4.1.2 Por que fazer?

Visualizações estão presentes na grande maioria dos projetos de ciência de dados. Além disso, é a parte mais acessível da ciência de dados do ponto de vista de quem lê. Mostrar uma visualização costuma ser mais efetivo do que a saída de um modelo ou uma fórmula. Finalmente, é uma das partes mais difíceis de automatizar da ciência de dados. Uma carreira em dataviz dificilmente ficará obsoleta.

4.1.3 Para que servem?

Uma base de dados contém toda a informação que precisamos. No entanto, não somos capazes de tirar conclusões apenas olhando essas bases. Por isso, é necessário resumir esses dados em estatísticas, como vimos na apostila sobre medidas de posição e variabilidade. Nem sempre as estatísticas (os números) são úteis para uma comunicação efetiva… Por isso, faz sentido mostrá-las usando formas, cores e outros elementos que facilitam a absorção da informação pelas pessoas.

4.1.4 Em que momento utilizamos?

Abaixo, temos o ciclo da ciência de dados. Esse diagrama foi adaptado do livro R para ciência de dados, que é uma referência para quem quer aprender ciência de dados com R.

Esse ciclo resume a maioria das tarefas que precisamos executar ao longo de um projeto de ciência de dados. Começamos pela importação, que envolve a leitura de dados de diferentes fontes. Em seguida, limpamos e transformamos esses dados para que possam ser usados em análises. A etapa de análise é um ciclo em si, envolvendo transformação de dados (criação de colunas e agregações), a visualização dos dados e a aplicação de modelos estatísticos / de machine learning para entender os dados. Finalmente, precisamos comunicar os resultados ou automatizar nosso produto de dados.

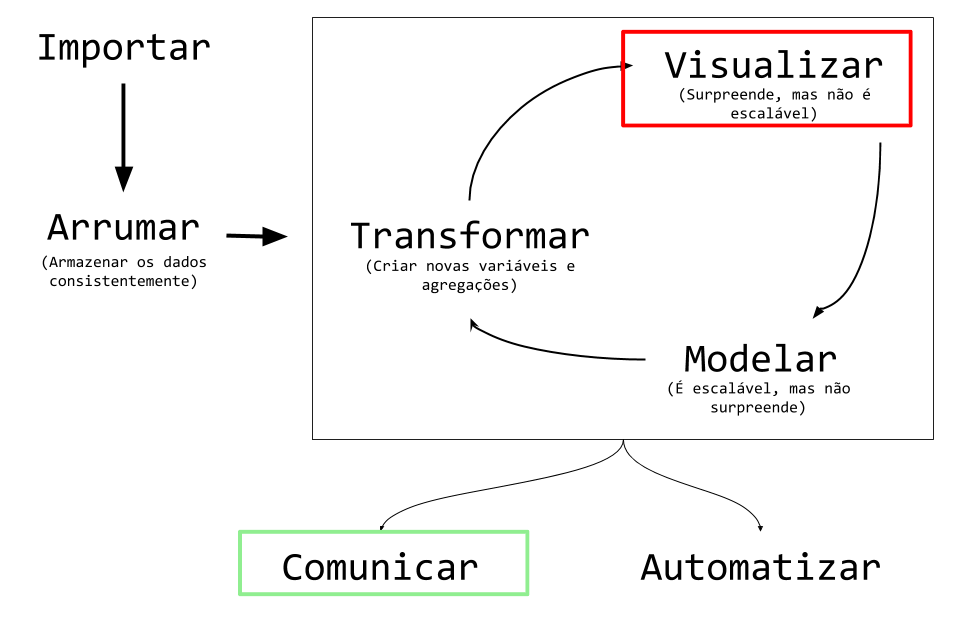
Note que a visualização de dados aparece em duas partes principais: Visualizar e Comunicar.

Na parte de visualização, estamos fazendo uma análise exploratória dos dados. Isso significa que estamos tentando entender os dados, e não necessariamente comunicar resultados. É um trabalho de investigação, que precisa ser rápido de fazer. O objetivo principal é aprender.

Na parte de comunicação, estamos fazendo um trabalho de otimização visual. Agora, nosso objetivo é comunicar os resultados com outras pessoas. Isso significa que precisamos de gráficos mais bonitos, mais explicativos e mais fáceis de entender. O trabalho deve, inclusive, ser encaixado em um fluxo de storytelling. O objetivo principal é comunicar.

O plotnine é uma biblioteca muito efetiva para fazer gráficos de análise exploratória e para otimização visual de gráficos estáticos. É possível fazer gráficos muito bonitos com ela, e é uma biblioteca muito fácil de usar. Por isso, é uma ótima escolha para começar a aprender visualização de dados. Ela é baseada em uma ferramenta muito popular e robusta da linguagem de programação R: o ggplot2. Atualmente, o plotnine é a biblioteca mais próxima do ggplot2 na linguagem Python e, mesmo não sendo tão completa quanto o ggplot2, já é suficiente para nossas aplicações.

A partir de agora, vamos retomar os nossos conceitos de tipos de variáveis e descrever as melhores visualizações para cada combinação de tipos de variáveis.

Uma referência legal nesse sentido é o site From Data to Viz, que é um guia para escolher a melhor visualização para os seus dados.

Vamos tratar dos seguintes exemplos:

1. Visualizações para variáveis categóricas

• Gráficos univariados
• Gráficos bivariados
  • Com outra categórica
  • Com variável numérica

2. Visualizações para variáveis numéricas

• Gráficos univariados
• Gráficos bivariados
  • Com variável categórica
  • Com outra numérica

Primeiro vamos ver gráficos exploratórios, depois vamos dar um exemplo de otimização visual.

4.2 Mapeamento estético

O plotnine é baseado na gramática dos gráficos (grammar of graphics), que é uma forma de pensar em gráficos de forma estruturada. A ideia central é que um gráfico é uma representação visual de dados. Assim, um gráfico é composto por:

• Dados: a base de dados que queremos representar
• Mapeamento estético: a relação entre as variáveis (colunas) da base de dados e os elementos visuais do gráfico (posição, cor, tamanho, forma)
• Geometria: os elementos visuais que compõem o gráfico (pontos, linhas, barras, caixas, etc)

O gráfico também pode ter outros componentes, como facetas, temas, rótulos, etc. No entanto, os três componentes acima são os mais importantes.

4.3 Visualizações para variáveis categóricas

Os gráficos univariados de variáveis categóricas são os mais comuns em ciência de dados no direito, já que o tipo de variável mais comum é a categórica.

4.3.1 Univariada

A função mais comum para visualizar variáveis categóricas é o countplot. Esse gráfico é uma versão do barplot do matplotlib, mas com a contagem de cada categoria no eixo y.

(
    ggplot(camaras) +  # dados
    aes(x='decisao') + # mapeamento estético
    geom_bar()         # geometria
)

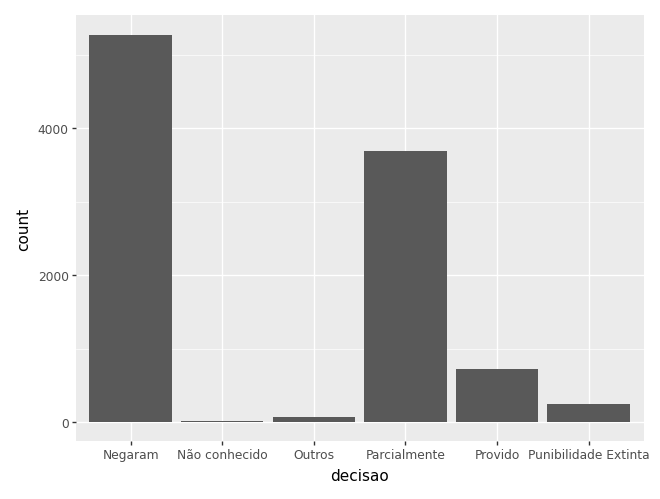
Outra forma de visualizar é rotacionando o eixo:

(
    ggplot(camaras) +  # dados
    aes(x='decisao') + # mapeamento estético
    geom_bar() +       # geometria
    coord_flip()
)

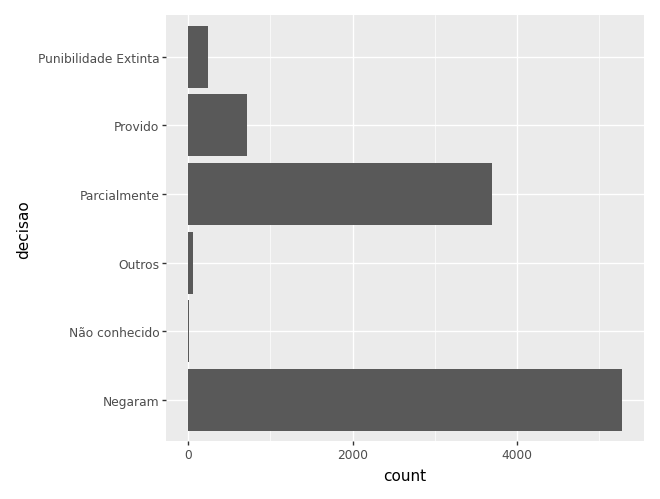
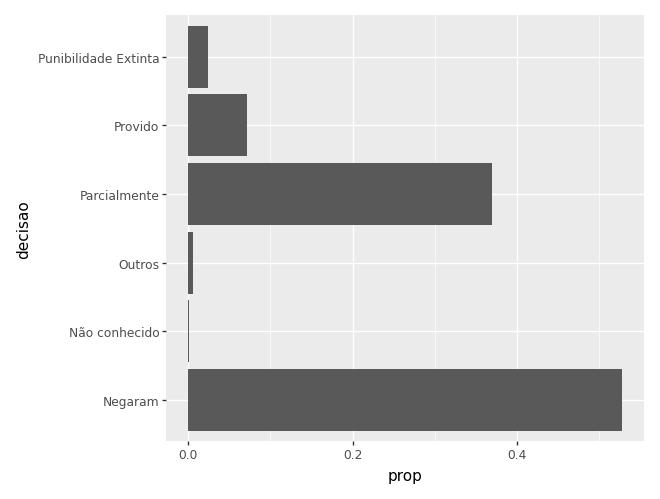
Se nosso interesse é mostrar a proporção e não os valores absolutos, podemos calcular as proporções e depois utilizar um gráfico de barras com geom_col():

dados_agregados = camaras.value_counts('decisao').reset_index(name='n')
dados_agregados['prop'] = dados_agregados['n'] / dados_agregados['n'].sum()

(
    ggplot(dados_agregados) +
    aes(x='decisao', y='prop') +
    geom_col() +
    coord_flip()
)

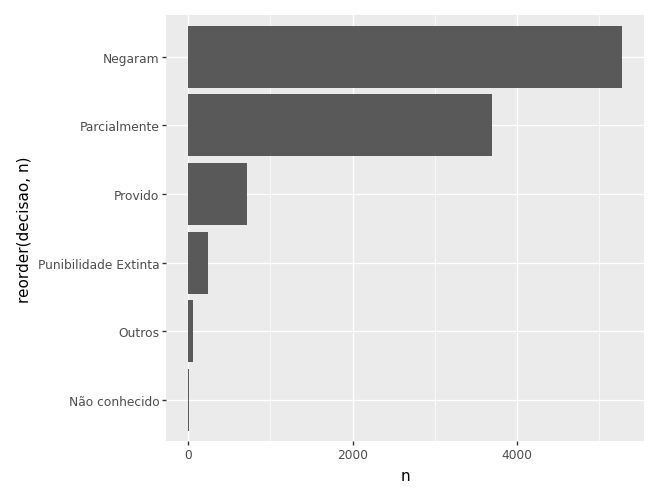
Também podemos ordenar as barras para facilitar a leitura. Duas formas de fazer isso são:

• Usando a função reorder() (mais fácil).
• Transformando a variável categórica em um tipo category do pandas, e ordenando as categorias (mais robusto).

# usando reorder

dados_agregados = camaras.value_counts('decisao').reset_index(name='n')
dados_agregados['prop'] = dados_agregados['n'] / dados_agregados['n'].sum()

(
    ggplot(dados_agregados) +
    aes(x='reorder(decisao, n)', y='n') +
    geom_col() +
    coord_flip()
)

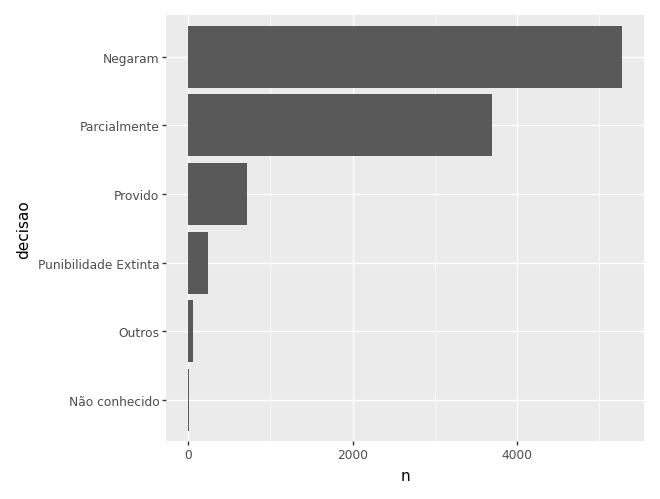
# usando categoria ordenada

dados_agregados = camaras.value_counts('decisao').reset_index(name='n')
dados_agregados['prop'] = dados_agregados['n'] / dados_agregados['n'].sum()

dados_agregados['decisao'] = pd.Categorical(
    dados_agregados['decisao'], 
    categories=dados_agregados.sort_values('n')['decisao']
)

(
    ggplot(dados_agregados) +
    aes(x='decisao', y='n') +
    geom_col() +
    coord_flip()
)

4.3.2 Bivariada: explicativa categórica

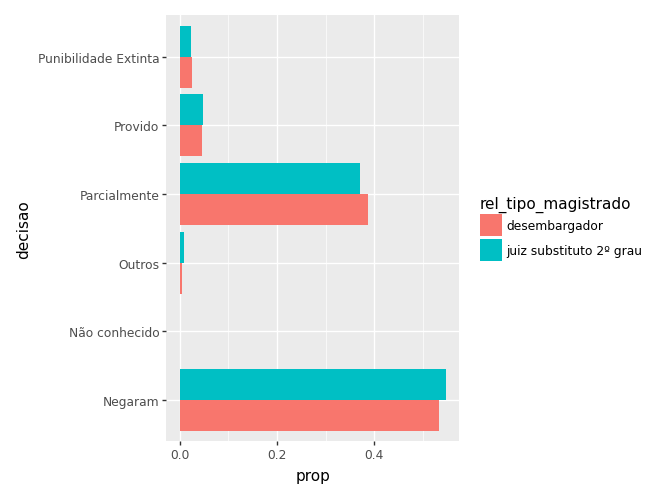
Quando temos duas variáveis categóricas, temos várias escolhas de visualizações possíveis para os gráficos de barras. Os mais comuns são i) separar por cores e colocar as barras lado a lado; ii) separar por cores e empilhar as barras; e iii) criar sub-gráficos para cada categoria.

Barras lado a lado

ct_mag = (
  camaras
  .query('polo_mp == "Passivo"')
  .value_counts(['rel_tipo_magistrado', 'decisao'])
  .reset_index(name='n')
)

ct_mag['prop'] = ct_mag['n'] / ct_mag.groupby('rel_tipo_magistrado')['n'].transform('sum')

ct_mag

	rel_tipo_magistrado	decisao	n	prop
0	desembargador	Negaram	4259	0.533041
1	desembargador	Parcialmente	3098	0.387735
2	juiz substituto 2º grau	Negaram	656	0.547123
3	juiz substituto 2º grau	Parcialmente	445	0.371143
4	desembargador	Provido	370	0.046308
5	desembargador	Punibilidade Extinta	205	0.025657
6	juiz substituto 2º grau	Provido	58	0.048374
7	desembargador	Outros	45	0.005632
8	juiz substituto 2º grau	Punibilidade Extinta	28	0.023353
9	desembargador	Não conhecido	13	0.001627
10	juiz substituto 2º grau	Outros	10	0.008340
11	juiz substituto 2º grau	Não conhecido	2	0.001668

(
    ggplot(ct_mag) +
    aes(x='decisao', y='prop', fill='rel_tipo_magistrado') +
    geom_col(position='dodge') +
    coord_flip()
)

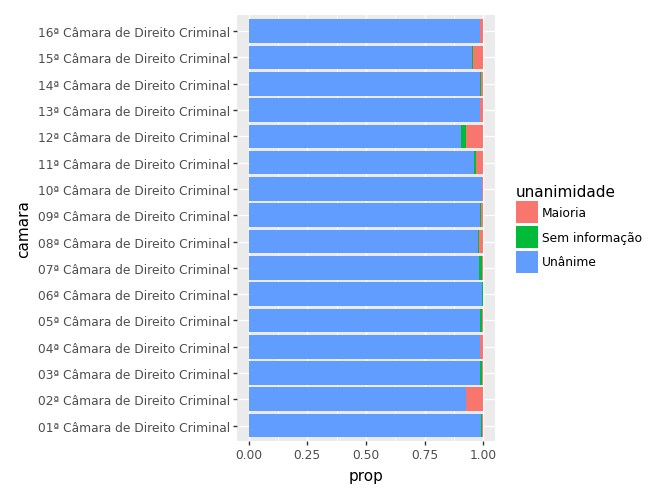
Barras empilhadas

camaras['extraord'] = camaras['camara'].str.contains('Extra')

ct_cam = (
  camaras
  .query('polo_mp == "Passivo"')
  .query('extraord == False')
  .value_counts(['camara', 'unanimidade'])
  .reset_index(name='n')
)

ct_cam['prop'] = ct_cam['n'] / ct_cam.groupby('camara')['n'].transform('sum')

ct_cam.head(10)

	camara	unanimidade	n	prop
0	06ª Câmara de Direito Criminal	Unânime	661	0.995482
1	08ª Câmara de Direito Criminal	Unânime	621	0.977953
2	07ª Câmara de Direito Criminal	Unânime	587	0.979967
3	16ª Câmara de Direito Criminal	Unânime	579	0.983022
4	13ª Câmara de Direito Criminal	Unânime	575	0.984589
5	14ª Câmara de Direito Criminal	Unânime	567	0.986087
6	09ª Câmara de Direito Criminal	Unânime	551	0.985689
7	15ª Câmara de Direito Criminal	Unânime	538	0.952212
8	11ª Câmara de Direito Criminal	Unânime	531	0.960217
9	04ª Câmara de Direito Criminal	Unânime	525	0.983146

(
    ggplot(ct_cam) +
    aes(x='camara', y='prop', fill = 'unanimidade') +
    geom_col() +
    coord_flip()
)

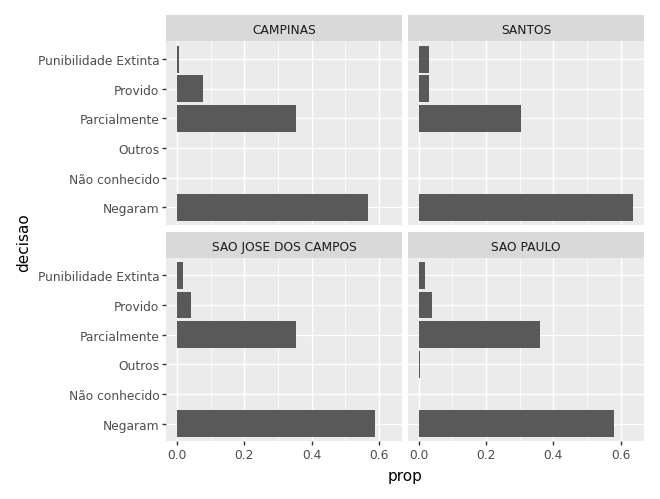
Sub-gráficos (facets)

Para facer sub-gráficos com o plotnine, podemos usar a função facet_wrap(). Ela cria um sub-gráfico para cada categoria de uma variável categórica.

comarcas = ['SAO PAULO', 'SAO JOSE DOS CAMPOS', 'SANTOS', 'CAMPINAS']

ct_comarca = (
  camaras
  .query('polo_mp == "Passivo"')
  .query('comarca in @comarcas')
  .value_counts(['comarca', 'decisao'])
  .reset_index()
)

ct_comarca['prop'] = ct_comarca['count'] / ct_comarca.groupby('comarca')['count'].transform('sum')

ct_comarca

	comarca	decisao	count	prop
0	SAO PAULO	Negaram	1061	0.579465
1	SAO PAULO	Parcialmente	657	0.358820
2	CAMPINAS	Negaram	127	0.566964
3	CAMPINAS	Parcialmente	79	0.352679
4	SAO JOSE DOS CAMPOS	Negaram	70	0.588235
5	SAO PAULO	Provido	69	0.037684
6	SANTOS	Negaram	63	0.636364
7	SAO JOSE DOS CAMPOS	Parcialmente	42	0.352941
8	SAO PAULO	Punibilidade Extinta	36	0.019661
9	SANTOS	Parcialmente	30	0.303030
10	CAMPINAS	Provido	17	0.075893
11	SAO PAULO	Outros	7	0.003823
12	SAO JOSE DOS CAMPOS	Provido	5	0.042017
13	SANTOS	Punibilidade Extinta	3	0.030303
14	SANTOS	Provido	3	0.030303
15	SAO JOSE DOS CAMPOS	Punibilidade Extinta	2	0.016807
16	CAMPINAS	Punibilidade Extinta	1	0.004464
17	SAO PAULO	Não conhecido	1	0.000546

(
    ggplot(ct_comarca) +
    aes(x='decisao', y='prop') +
    geom_col() +
    facet_wrap('~comarca') +
    coord_flip()
)

4.3.3 Bivariada: explicativa numérica

Quando temos a variável de interesse categórica e a explicativa numérica, é um pouco difícil de criar visualizações, porque no fundo o que queremos entender é como o aumento/diminuição dessa variável numérica afeta a probabilidade de um evento relacionado à variável categórica acontecer. Isso geralmente é feito através de modelos estatísticos como a regressão logística, que veremos mais para frente na disciplina.

Algumas alternativas são: i) categorizar a variável numérica – nesse caso, voltamos ao que já vimos anteriormente; ii) analisar a distribuição da variável numérica para cada categoria – nesse caso, é como se estivéssemos invertendo qual é a variável de interesse e qual é a variável explicativa, logo isso faz parte da seção de variáveis numéricas, que veremos ainda nessa apostila, mas mais para frente.

4.4 Visualização para variáveis numéricas

4.4.1 Univariada

A análise univariada de uma variável de interesse numérica geralmente busca entender a distribuição dos dados.

Existem três principais visualizações aqui: histograma, densidade e boxplot. A densidade é simplesmente uma versão suavizada do histograma, e é possível mostrar os dois ao mesmo tempo.

(
    ggplot(camaras) +
    aes(x='tempo') +
    geom_histogram(binwidth=1)
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_bin : Removed 1 rows containing non-finite values.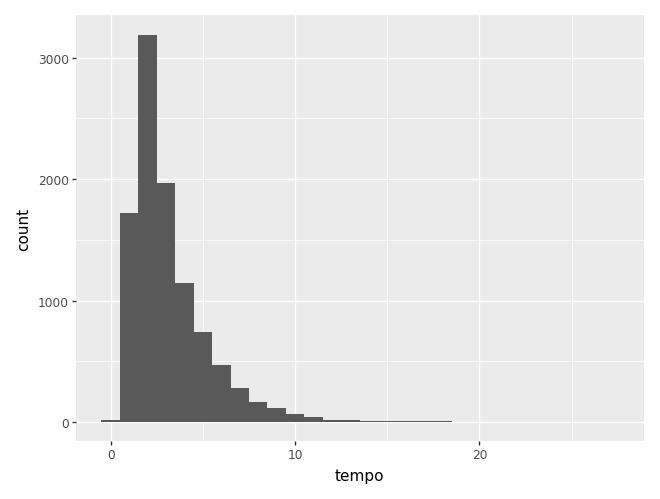

Podemos mudar o número de barras com os parâmetros bins (quantidade de barras) ou binwidth (largura da barra).

(
    ggplot(camaras) +
    aes(x='tempo') +
    geom_histogram(bins=40)
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_bin : Removed 1 rows containing non-finite values.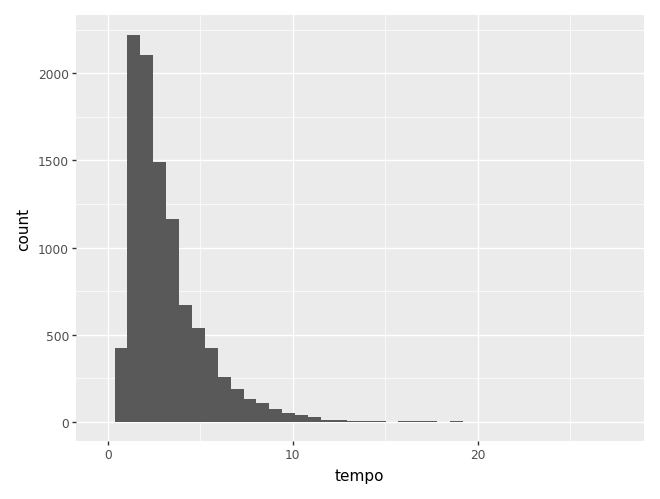

Densidade:

(
    ggplot(camaras) +
    aes(x='tempo') +
    geom_density()
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_density : Removed 1 rows containing non-finite values.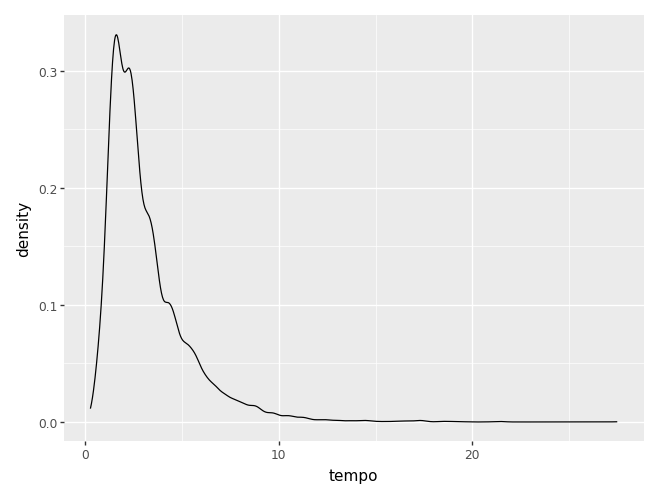

Veja que, nesse caso, o eixo y representa a densidade, e não as contagens. A densidade tem relação com o conceito de distribuição de probabilidades. Na verdade, essa densidade é uma estimativa da função densidade de probabilidades da variável estudada (ou seja, é um modelo estatístico!). A área total do gráfico é 1.

Abaixo, juntamos histograma e densidade

(
    ggplot(camaras) +
    aes(x='tempo') +
    geom_histogram(binwidth=1) +
    geom_density(aes(y=after_stat('count')), alpha=0.2, fill = 'red')
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_bin : Removed 1 rows containing non-finite values.
c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_density : Removed 1 rows containing non-finite values.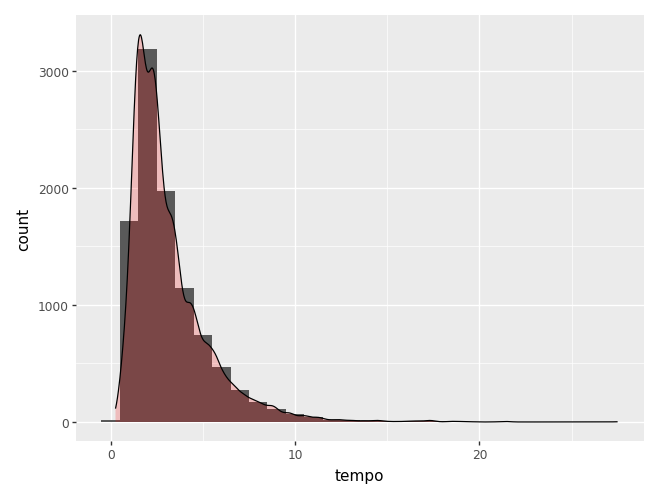

Finalmente, temos o boxplot. O boxplot pode ser usado no caso univariado, mas é mais comum quando temos uma variável explicativa categórica.

(
    ggplot(camaras, aes(y='tempo')) +
    geom_boxplot() +
    coord_flip()
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_boxplot : Removed 1 rows containing non-finite values.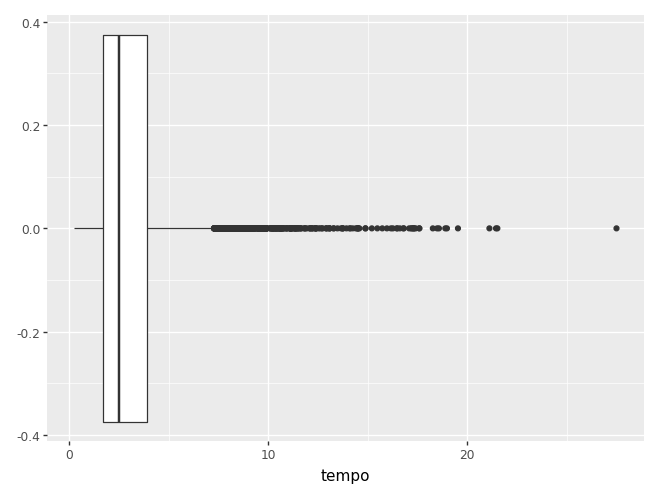

4.4.2 Bivariada: explicativa categórica

A ideia aqui é simplesmente repetir os gráficos acima para a variável categórica de interesse.

Começamos pelo histograma / densidade

(
    ggplot(camaras) +
    aes(x='tempo') +
    geom_histogram(bins=30) +
    facet_wrap('~decisao')
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_bin : Removed 1 rows containing non-finite values.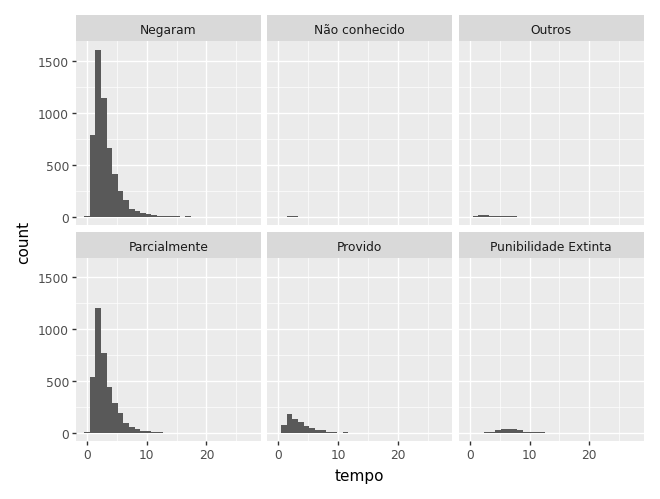

Note que aqui, a escala pode afetar o gráfico e dificultar a comparação.

(
    ggplot(camaras) +
    aes(x='tempo') +
    geom_histogram(bins=30) +
    facet_wrap('~decisao', scales='free_y')
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_bin : Removed 1 rows containing non-finite values.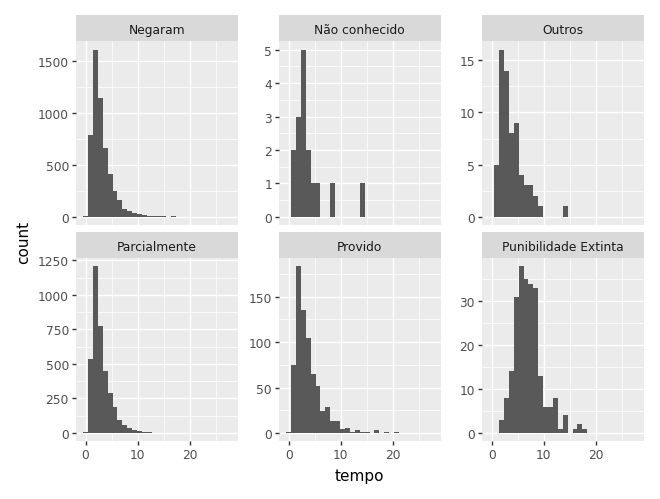

Quando temos muitas categorias, o gráfico fica difícil de interpretar. Nesse caso, o boxplot é uma alternativa melhor.

camaras_sem_extraord = camaras[~camaras['extraord']].sort_values('camara')

(
    ggplot(camaras_sem_extraord) +
    aes(x='camara', y='tempo') +
    geom_boxplot() +
    coord_flip()
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_boxplot : Removed 1 rows containing non-finite values.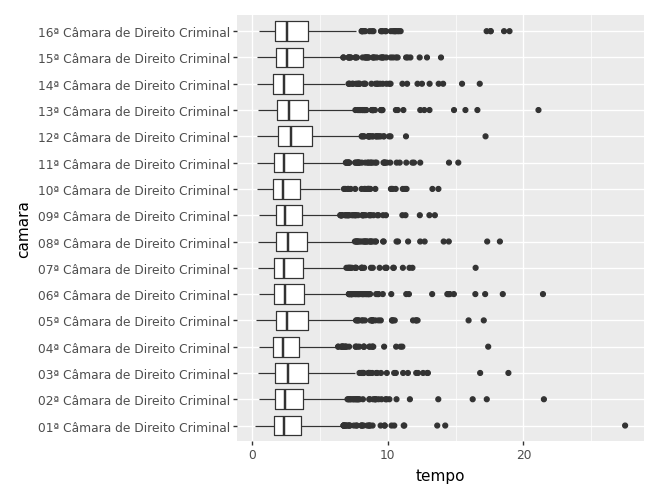

# alternativa ao boxplot: violinplot
# trata-se basicamente de um gráfico de densidade duplicado. Fica bonitinho.

(
    ggplot(camaras_sem_extraord) +
    aes(x='camara', y='tempo') +
    geom_violin(draw_quantiles=0.5) +
    coord_flip()
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:293: PlotnineWarning: stat_ydensity : Removed 1 rows containing non-finite values.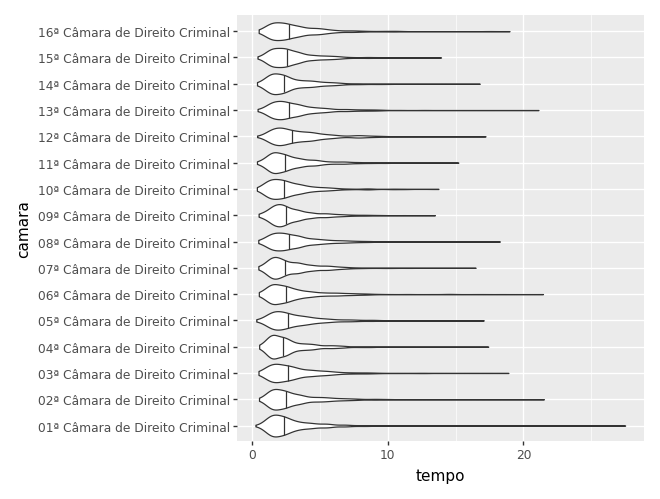

4.4.3 Bivariada: explicativa numérica

Quando temos duas variáveis numéricas, usualmente fazemos um gráfico de dispersão. Nesse caso, usamos o geom_point().

(
    ggplot(camaras) +
    aes(x='rel_tempo_magistratura', y='tempo') +
    geom_point()
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:372: PlotnineWarning: geom_point : Removed 2733 rows containing missing values.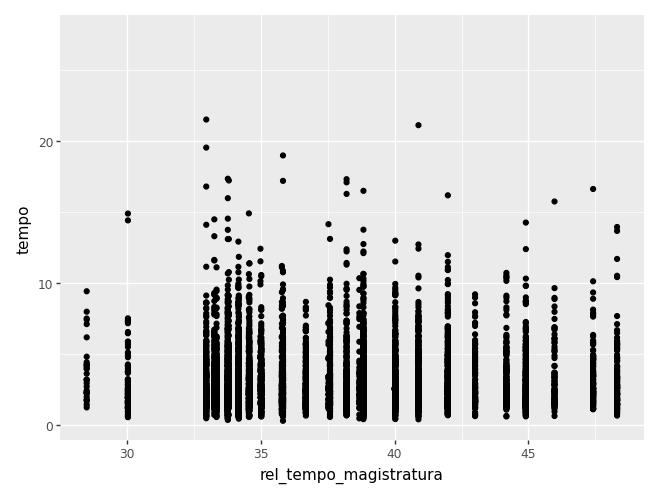

Podemos até adicionar mais variáveis aqui, como, por exemplo, nas cores

(
    ggplot(camaras) +
    aes(x='rel_tempo_magistratura', y='tempo', colour='rel_quinto') +
    geom_point()
)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\layer.py:372: PlotnineWarning: geom_point : Removed 2733 rows containing missing values.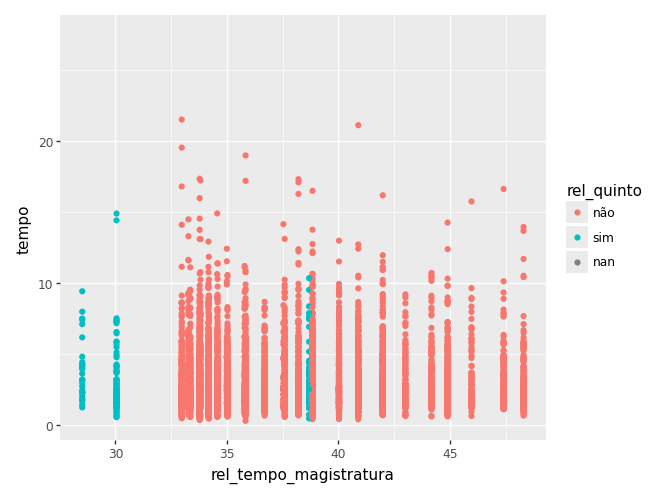

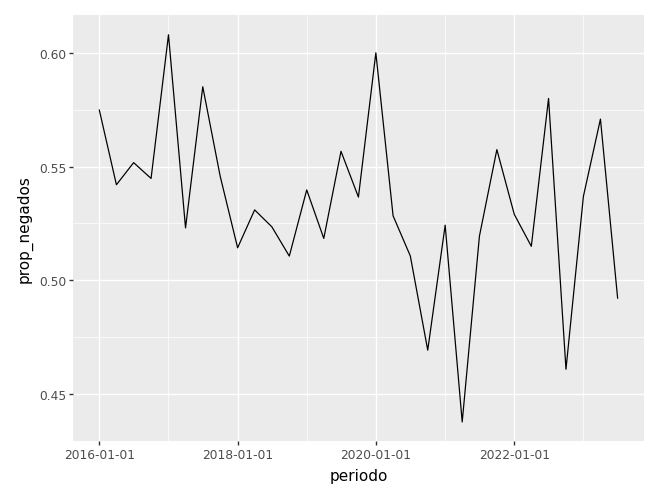
Um tipo especial de análise bivariada é quando o eixo x é uma data. Nesse caso, temos uma série de tempo, e representsaos os dados com um gráfico de linhas.

# vamos calcular a proporção de negados ao longo do tempo

# criando uma coluna que pega a data de publicação e arredonda o trimestre
# o pandas é bem burocrático para fazer essa tarefa simples
camaras['periodo'] = pd.to_datetime(camaras['dt_publicacao']).dt.to_period('Q').dt.to_timestamp()

prop_negados_mes = (
    camaras
    .query('polo_mp == "Passivo"')
    .groupby('periodo')
    .agg(prop_negados = ('decisao', lambda x: (x == 'Negaram').mean()))
    .reset_index()
)

(
    ggplot(prop_negados_mes) +
    aes(x='periodo', y='prop_negados') +
    geom_line()
)

4.5 Otimização

A otimização visual é um assunto extenso e muito baseado em tentativa e erro. Afinal, o que queremos aqui é adaptar nosso gráfico para um fim específico, e isso pode variar muito. Nessas situações, o chatGPT e ferramentas similares podem ser muito úteis!

Vamos colocar alguns exemplos de otimização aqui:

• Colocar o % nos eixos que são porcentagens
• Mudar o título dos eixos
• Mudar as cores das barras
• Mudar a cor de fundo

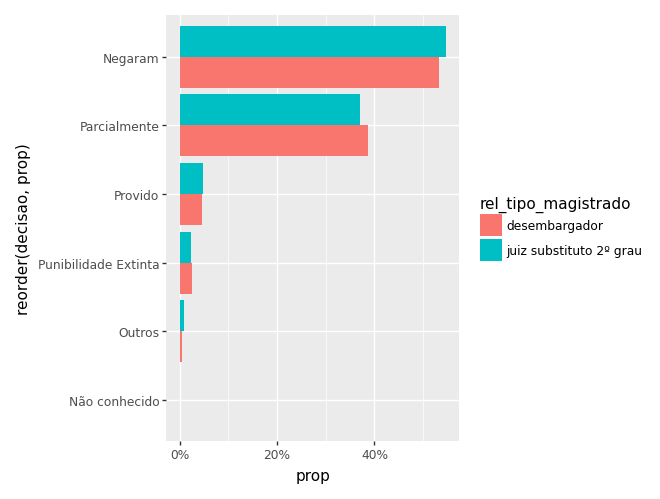
Colocar o % nos eixos que são porcentagens

Vamos voltar para o gráfico que vimos anteriormente

from mizani.labels import percent_format

(
    ggplot(ct_mag) +
    aes(x='reorder(decisao, prop)', y='prop', fill='rel_tipo_magistrado') +
    geom_col(position='dodge') +
    coord_flip() +
    scale_y_continuous(labels=percent_format())
)

Veja que precisamos voltar a usar uma função mais ‘baixo nível’, a barplot

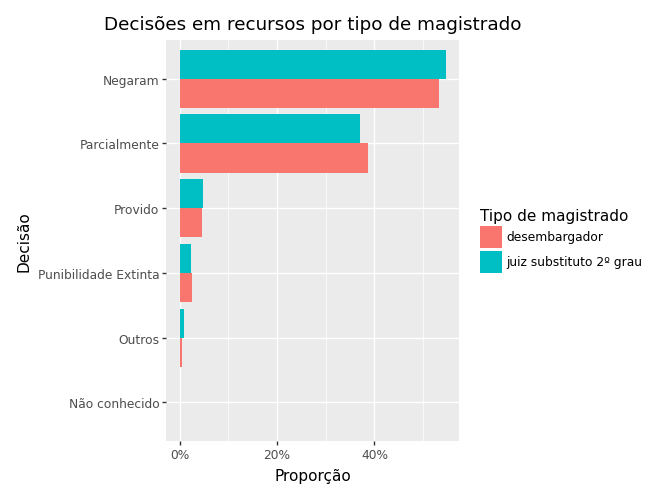
Mudar o título dos eixos

(
    ggplot(ct_mag) +
    aes(x='reorder(decisao, prop)', y='prop', fill='rel_tipo_magistrado') +
    geom_col(position='dodge') +
    coord_flip() +
    scale_y_continuous(labels=percent_format()) +
    labs(
        title='Decisões em recursos por tipo de magistrado',
        x='Decisão',
        y='Proporção',
        fill='Tipo de magistrado'
    )
)

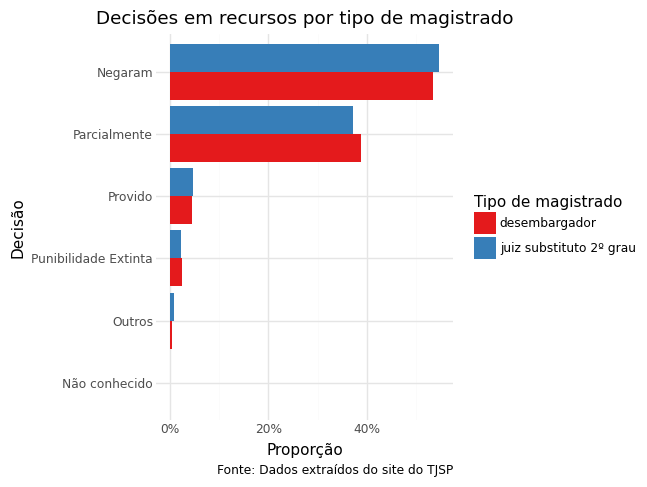
Cores

(
    ggplot(ct_mag) +
    aes(x='reorder(decisao, prop)', y='prop', fill='rel_tipo_magistrado') +
    geom_col(position='dodge') +
    coord_flip() +
    scale_y_continuous(labels=percent_format()) +
    labs(
        title='Decisões em recursos por tipo de magistrado',
        x='Decisão',
        y='Proporção',
        fill='Tipo de magistrado',
        caption='Fonte: Dados extraídos do site do TJSP'
    ) +
    theme_minimal() +
    scale_fill_brewer(type='qual', palette='Set1')
)

grafico_otimizado = (
    ggplot(ct_mag) +
    aes(x='reorder(decisao, prop)', y='prop', fill='rel_tipo_magistrado') +
    geom_col(position='dodge') +
    coord_flip() +
    scale_y_continuous(labels=percent_format()) +
    labs(
        title='Decisões em recursos por tipo de magistrado',
        x='Decisão',
        y='Proporção',
        fill='Tipo',
        caption='Fonte: Dados extraídos do site do TJSP'
    ) +
    theme_minimal() +
    scale_fill_brewer(type='qual', palette='Set2') +
    theme(
        plot_title=element_text(hjust=0),
        legend_position='top'
    )
)

Salvando um gráfico em arquivo:

ggsave(grafico_otimizado, filename='grafico_otimizado.png', dpi=300, width=8, height=6)

c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\ggplot.py:630: PlotnineWarning: Saving 8 x 6 in image.
c:\Users\julio\OneDrive\Documentos\insper\cdad-book\.venv\Lib\site-packages\plotnine\ggplot.py:631: PlotnineWarning: Filename: grafico_otimizado.png